В практической работе с топографической картой часто приходится измерять расстояния как по прямой линии (определение дальности до целей, расстояний между местными предметами, координат точек), так и по извилистой линии (определение длины маршрута), а также измерять, вычислять различные углы.
Чтобы измерить расстояние по карте, нужно знать ее масштаб. Масштаб карты указывается под нижней рамкой карты и выражается численно — численный масштаб и графически — линейный масштаб (рис. 5).
Рис. 5. Численный и линейный масштабы карты
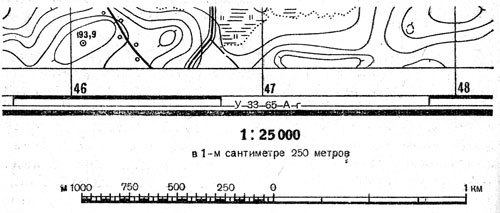
Чтобы определить по карте расстояние между местными предметами (точками местности) пользуясь численным масштабом, измеряют линейкой или циркулем расстояние между этими предметами (точками местности) в сантиметрах и умножают полученное число на величину масштаба. Например, по карте масштаба 1 : 25 000 расстояние между наблюдательными пунктами равно 5,5 см, а расстояние между этими пунктами на местности будет равно 5,5 X 250 = 1375 м.
При определении небольших расстояний между двумя точками проще пользоваться линейным масштабом. Для этого циркулем или линейкой измеряют на карте расстояние между этими точками и прикладывают его к линейному масштабу карты, по которому определяют искомое расстояние (в километрах и метрах) на местности.
При отсутствии циркуля и линейки расстояние между точками по карте можно определить по линейному масштабу, пользуясь ровной полоской бумаги. Для этого полоску бумаги прикладывают к точкам на карте, между которыми определяют расстояние, и против этих точек на бумаге делают отметки в виде штрихов. Приложив отмеченный штрихами отрезок бумаги к линейному масштабу, определяют расстояние между этими точками на местности.
На крупномасштабных картах часто приходится определять координаты точек (целей, ориентиров, элементов боевого порядка своих войск и войск противника).
Координатами точки называют угловые или линейные величины, характеризующие ее положение на поверхности или в пространстве.
Поскольку определение координат по карте очень распространено, подробно этот вопрос будет изложен в разделе 9.
При измерении расстояний для определения координат точек пользуются так называемой координатной меркой (рис. 6) или координатомером (рис. 7), которые несколько упрощают работу, заменяя при этом масштаб, циркуль и линейку.
Рис. 6. Координатная мерка

Рис. 7. Координатомер и пользование им для определения координат точки на карте
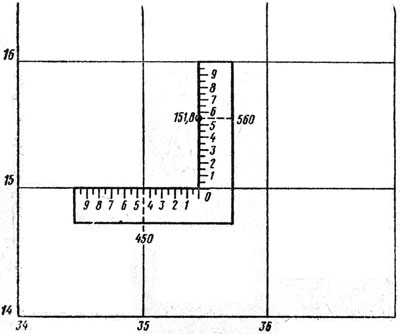
Координатная мерка представляет собой прозрачную целлулоидную пластинку с координатной сеткой. Две взаимно перпендикулярные линии делят координатную сетку на четыре равных квадрата; эти линии оканчиваются стрелками, имеющими обозначения: С (север), Ю (юг), В (восток) и 3 (запад). Расстояние между линиями сетки равно 2 мм; цена делений сетки для карт масштабов 1 : 25 000 и 1 : 50 000 соответственно равна 50 и 100 м. В северо-восточной части сетки выделен жирными линиями квадрат со сторонами в 2 см. На углах пластинки имеются шкалы, служащие для определения координат точек карты при разных ее масштабах. Шкалы для масштабов 1 : 25 000 и 1 : 50 000 имеют миллиметровые деления и оцифрованы в сотнях метров: шкала для масштаба 1 : 42 000, оцифрованная через 0,2 дюйма, предназначается для старых карт, разграфленных на дюймовые и двухдюймовые квадраты. В центре пластинки имеется отверстие для накола точек при нанесении их на карту.
Координатомер имеет вид угольника, на внутренних сторонах которого нанесены миллиметровые деления, оцифрованные в сотнях метров.
Если расстояния между штрихами делений равны 2 мм, то цена деления для карт масштабов 1 : 25 000 и 1 : 50 000 соответственно равна 50 и 100 м.
Координатомеры любого масштаба легко изготовить из картона, пластика или целлулоида.
Большие расстояния по прямым линиям измеряют на карте по частям. Для этого по масштабу устанавливают раствор циркуля, соответствующий целому числу километров, и этим раствором измеряют на карте заданное расстояние. При этом отрезок на конце измеряемого расстояния, не укладывающийся в растворе циркуля, определяют с помощью линейного масштаба и полученное значение прибавляют к отсчитанному числу километров.
Таким же способом измеряют расстояния по кривым и извилистым линиям. В этом случае раствор циркуля делают небольшим в зависимости от степени извилистости измеряемого расстояния.
Для удобства определения длины маршрута, особенно по длинным и извилистым линиям, пользуются специальным прибором- курвиметром (рис. 8).
Рис. 8. Курвиметр
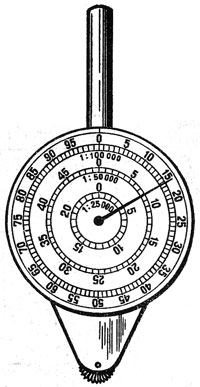
Прибор представляет собой круглую коробочку с держателем. В центре прибора находится циферблат со стрелкой, внизу имеется колесико, при помощи которого обводится маршрут. Колесико соединено системой передач со стрелкой на циферблате, которая ведет отсчет величины пройденного расстояния по карте.
Деления на шкале циферблата бывают различные: на одних курвиметрах они обозначают путь, проходимый колесиком по карте, в сантиметрах, на других — показывают непосредственно расстояние на местности в километрах в зависимости от масштаба карты. На рисунке показан курвиметр с тремя шкалами различных масштабов (1 : 100 000, 1 : 50 000, 1 : 25 000). Деления на шкалах показывают расстояния на местности в километрах.
Для определения длины маршрута с помощью курвиметра стрелку прибора устанавливают на нулевое положение циферблата. Затем курвиметр ставят вертикально колесиком на начальную точку маршрута и с равномерным нажимом прокатывают его вдоль маршрута так, чтобы показания стрелки возрастали. В конечной точке маршрута снимают отсчет по нужной шкале циферблата. Длина маршрута равна отсчету, умноженному на цену деления шкалы. Если курвиметр дает показания в сантиметрах, то для получения соответствующего им расстояния на местности умножают отсчет по шкале на величину масштаба карты.
По карте можно определять расстояния и приближенно. Для этого обычно используют километровую сетку.
Однако точность определения расстояний этим способом небольшая.
Точность определения расстояний по карте зависит от многих причин: от масштаба карты и ее качества, от характера измеряемых расстояний и точности их измерения, от рельефа местности.
Точность измерения расстояний по линейному масштабу ограничивается тем, что делить его основание на очень мелкие части нельзя, так как это затруднит отсчет. Для повышения точности измерений применяют так называемый поперечный масштаб.
Поперечный масштаб представляет собой прямоугольник (рис. 9), горизонтальная сторона которого разделена на несколько равных частей, обычно, по 2 см каждая.
Рис. 9. Поперечный масштаб
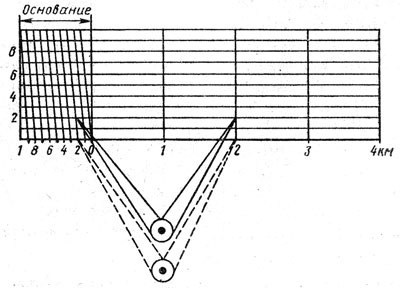
Каждая такая часть называется основанием масштаба. Крайнее левое основание в верхней и нижней частях поперечного масштаба делится на десять равных частей. Концы этих десятых долей основания соединяются между собой прямыми, отсекающими на горизонтальных линиях сотые доли основания.
Таким образом, на поперечном масштабе измеряемое расстояние может быть выражено в целых, десятых и сотых долях основания масштаба. А поскольку известна величина основания масштаба (2 см), то можно легко определить «цену» основания в метрах. Так, для масштаба 1 : 25 000 «цена» основания поперечного масштаба составит 500 м, его десятая доля — 50 м, а одна сотая часть — 5 м. Кроме того, на глаз можно взять еще и половину «сотни» — 2,5 м.
На рис. 9 показано, как надо пользоваться поперечным масштабом. Циркулем измеряют расстояние между двумя предметами на карте. Затем прикладывают циркуль к нижней линии поперечного масштаба и отсчитывают расстояние, которое получается — 2200 м с излишком. Для определения величины этого излишка циркуль передвигают параллельно нижней линии вверх До пересечения с диагональю и считывают окончательную величину расстояния — 2220 м.
Ориентирование на местности, а также решение многих специальных задач осуществляется посредством азимутов и дирекциониых углов направлений.
Поясним, что такое азимут и дирекционный угол.
Существует два вида азимутов: азимут истинный (А) и азимут магнитный (Ам).
Истинным азимутом называется угол между северным направлением географического (истинного) меридиана и направлением на местный предмет, отсчитанный по ходу часовой стрелки.
Магнитным азимутом называется угол, отсчитанный по ходу часовой стрелки от северного направления магнитного меридиана до направления на местный предмет; магнитный азимут всегда определяется с помощью магнитной стрелки.
Дирекционный угол (а) — это угол между северным направлением вертикальной линии координатной (километровой) сетки и направлением на местный предмет, отсчитанный по ходу часовой стрелки.
Определение азимутов и дирекционных углов направлений, а также углов между местными предметами связано с измерением этих углов на карте и местности.
Углы на карте и местности измеряют в градусной системе, а также в делениях угломера.
Одно деление угломера — это величина центрального угла, который соответствует дуге в 1/6000 окружности. Длина дуги, соответствующая углу в одно деление угломера, равна
![]()
С достаточным для практики округлением принимают, что длина этой дуги равна 1/1000 радиуса данной окружности. Этим и объясняется другое, часто употребляемое наименование деления угломера — тысячная.
На практике иногда применяют термины «малое деление угломера» и «большое деление угломера». «Малым делением угломера» называют одно деление угломера (одну «тысячную дальности»), «большим делением-100 делений угломера (100 «тысячных дальности»).
Так как окружность содержит 360″ или 360*60 = 21 600′, то одно деление угломера равно 21600/6000= 3′,6, а 100 делений (одно большое деление угломера) равны 3′,6*100 = 360′ = 6°.
Для системы измерения углов в тысячных существует простая зависимость между угловыми и линейными величинами, а именно: угловое расстояние между двумя равноудаленными от наблюдателя местными предметами равно линейному расстоянию между ними, умноженному на 1000 и деленному на величину дальности. Эта зависимость выражается формулой
![]()
где а — угловое расстояние между местными предметами в делениях угломера;
l — линейное расстояние между местными предметами в метрах;
Д- расстояние от наблюдателя до местных предметов в метрах.
Пример. Расстояние от наблюдателя до линии электропередачи Д = 500 м; линейное расстояние между столбами l = 50 м. Определить угловое расстояние а между этими столбами.
Решение:
![]()
Пользуясь приведенной формулой, можно определить линейное расстояние между предметами, если известны дальность до них и измерен угол
![]()
Если определено линейное и угловое расстояние между двумя предметами, то дальность до них
![]()
Величины углов, измеренных в тысячных, произносят, разделяя число сотен и число единиц. Например, величину угла в 1235 делений угломера записывают 12-35, а произносят «двенадцать тридцать пять». Угол в 38 делений угломера записывают 0-38, а произносят «ноль тридцать восемь», угол в 300 тысячных записывают 3-00, а произносят «три ноль» и т. д.
Для измерения и построения углов на карте пользуются транспортирами и целлулоидными кругами. Для более точных измерений и построений углов применяют специальные хордоугломеры.
Хордоугломер представляет собой латунную хромированную пластинку, на одной стороне которой нанесен собственно хордоугломер, а на другой — два поперечных масштаба.
Собственно хордоугломер (рис. 10)-это график хорд для углов, выраженных в делениях угломера, построенный по принципу поперечного масштаба.
Рис.10. Хордоугломер
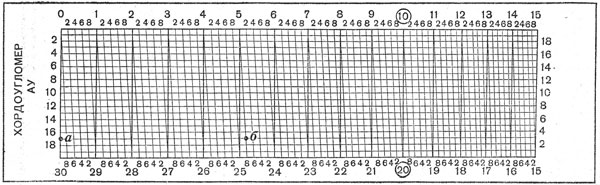
Способ измерения и построения углов по хордам основан на том, что каждому острому углу (до 15-00) соответствует определенной величины хорда окружности, проведенной из вершины угла.
По верхней горизонтальной линии графика от начальной точки отложены хорды, соответствующие углам через 0-20. У концов хорд, соответствующих углам от 1-00 до 15-00, написаны числа от «1» до «15».
Каждое большое деление на верхней горизонтальной линии графика разделено на пять малых делений ценой 0-20, обозначенных цифрами «2». «4», «6», «8», что соответствует 0-20, 0-40, 0-60, 0-80. Слева на вертикальной линии графика на концах четных горизонтальных линий проставлены числа «2», «4», «6»… до «18», соответствующие 0-02, 0-04, 0-06 и т. д.
Тупые углы (от 15-00 до 30-00) находят путем измерения соответствующего дополнительного до 30-00 угла.
Для отыскания хорд острых углов, дополнительных до 30-00, большие деления нижней горизонтальной линии оцифрованы справа налево числами «15», «16», «17»… до «30», а деления правой вертикальной линии графика — снизу вверх числами «2», «4», «6»… до «18».
Порядок измерения углов на карте с помощью хордо-угломера следующий (рис. 11).
Рис.11. Измерение углов на карте с помощью хордоугломера
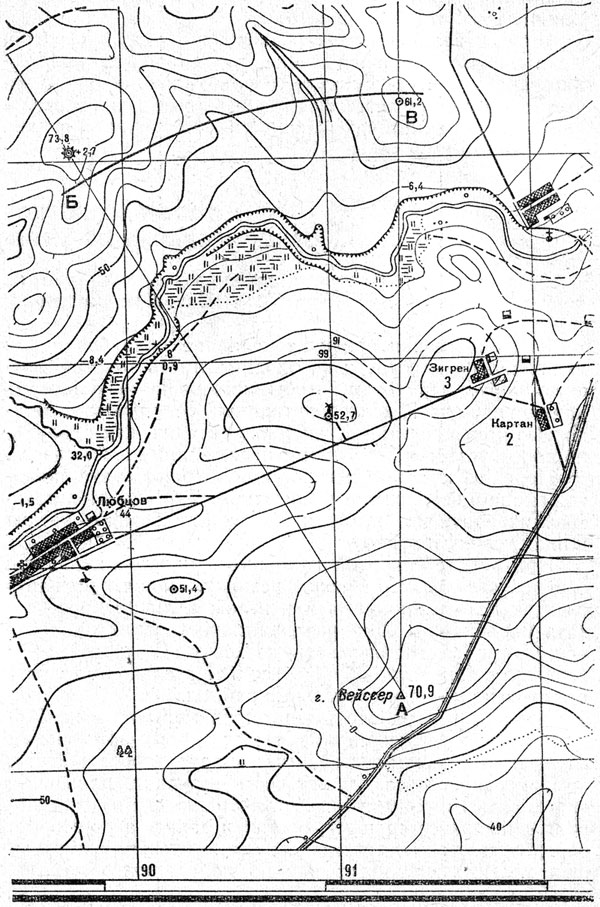
Из вершины измеряемого угла А при помощи циркуля проводят дугу радиусом, равным хорде угла 10-00 на хордоугломере. Циркулем берут величину хорды БВ измеряемого угла и переносят его на хордоугломер.
Расположив левую ножку циркуля в нулевой точке левой вертикальной линии графика хордоугломера, а правую ножку на верхней горизонтальной линии, передвигают обе ножки по вертикали вниз. Передвижение происходит до тех пор, пока правая ножка циркуля не совпадет с пересечением одной из наклонных линий с одной из горизонтальных линий графика; при этом обе ножки циркуля должны быть на одной горизонтальной линии (точки а и б на рис. 10).
Читают величину угла по верхнему ряду цифр графика против наклонной линии, на которой расположилась правая ножка циркуля, и прибавляют к ней количество делений по левому ряду цифр против горизонтальной линии, на которой находятся обе ножки циркуля. Измеренный угол равен 5-17
| << к Оглавлению | Дальше >> |
Связанные статьи:
1. Что такое местность?
2. Назначение и содержание топографических карт
3. Классификация топографических карт
4. Подготовка карты к работе
5. Измерительные приемы, применяемые при работе с картой
6. Топографическое ориентирование по карте
7. Изучение местности по карте
8. Оценка маршрута движения, выбранного или назначенного по карте
9. Определение координат точек по карте
10. Целеуказание по карте
11. Топографическая привязка с помощью карты
12. Хранение и сбережение карт